Question

Click an item in the list or group of pictures at the bottom of the problem and, holding the button down, drag it into the correct position in the answer box. Release your mouse button when the item is place. If you change your mind, drag the item to the trashcan. Click the trashcan to clear all your answers.Prove: The median of a trapezoid equals half the sum of its bases.

Answer 1

In the given figure we can determine the coordinate of point M from the graph, we get:

`M=((d)/(2),(c)/(2))`

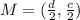
We can also determine the coordinates of point N as:

`N=((a+b)/(2),(c)/(2))`

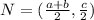
Now, to determine the length of segment MN, we need to subtract the x-coordinate of M from the coordinates of N, we get:

`MN=(a+b)/(2)-(d)/(2)`

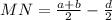
Subtracting the fractions we get:

`MN=(a+b-d)/(2)`

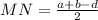
Now, to obtain the length of AB we need to subtract the x-coordinate of A from the x-coordinate of B.

The coordinates of A are determined from the graph:

`A=(0,0)`

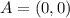
The coordinates of B are:

`B=(a,0)`

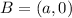
Therefore, the length of segment AB is:

`AB=a`

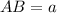
Now we do the same procedure to determine the segment of CD. The coordinates of C are:

`C=(b,c)`

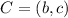
The coordinates of D are:

`D=(d,c)`

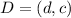
Therefore, CD is:

`CD=b-d`

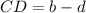
Now, we determine MN as half the sum of the bases. The bases are AB and CD, therefore:

`MN=(1)/(2)(a+b-d)`

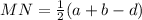
Therefore, we have proven that the median of a trapezoid equals half the sum of its bases.