Answer:
• (a)The probability that it will take on a value less than 1.64 is 0.9495.
,
• (b)The probability that it will take on a value greater than – 0.47 is 0.6808.
,
• (c)The probability that it will take on a value greater than 0.76 is 0.2236.
,
• (d)The probability that it will take on a value less than -1.35 is 0.0885
,
• (e)The probability that it will take on a value between 0.95 and 1.36 is 0.0841.
Explanation:
Given that a random variable has the standard normal distribution, then, we use a normal distribution table or calculator to find these values:
(a) Less than 1.64
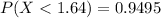
The probability that it will take on a value less than 1.64 is 0.9495.
(b)Greater than – 0.47
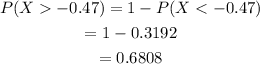
The probability that it will take on a value greater than – 0.47 is 0.6808.
(c)Greater than 0.76
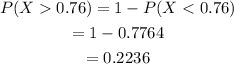
The probability that it will take on a value greater than 0.76 is 0.2236.
(d)Less than –1.35
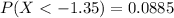
The probability that it will take on a value less than -1.35 is 0.0885
(e) Between 0.95 and 1.36
[tex]\begin{gathered} P\left(x<0.95\right)=0.8289 \\ P\left(x>1.36\right)=0.0869 \\ P\left(x<0.95\;or\;x>1.36\right)=0.8289+0.0869=0.9159 \\ P\left(0.95
The probability that it will take on a value between 0.95 and 1.36 is 0.0841.