Question

If g(x) = x - 11, Find g(x) = -7

Answer 1

By definition, the function is a relation in which each input value (x-value) has one and only one output value (y-value).

In this case, you have the following function:

`g\mleft(x\mright)=x-11`

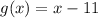
And you need to find the input value that has the following output value:

`g\mleft(x\mright)=-7​`

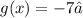
In order to find that value of "x", you need to substitute the given ouput value into the function:

`\begin{gathered} g\mleft(x\mright)=x-11 \\ -7=x-11 \end{gathered}`

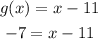
And now you must solve for the variable "x". To do it, you must apply the Addition property of equality by adding 11 to both sides of the equation:

`\begin{gathered} -7+(11)=x-11+(11) \\ x=4 \end{gathered}`

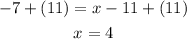
The answer is:

`x=4`