Question

how much must be deposited the beginning of each year in an account that pays 6% compounded annual so that the count will contain 22,000 at the end of four years

Answer 1

We know that

• The interest rate is 6% (0.06).

,

• The compounding period is annual. (n = 1).

,

• The final amount is $22,000.

,

• The time is 4 years. (t = 4).

Let's use the compound interest formula

`A=P(1+(r)/(n))^(nt)`

We have to replace the given values and solve for P

`\begin{gathered} 22,000=P(1+(0.06)/(1))^(1\cdot4) \\ 22,000=(1.26)P \\ P\approx(22,000)/(1.26) \\ P\approx17,460.32 \end{gathered}`

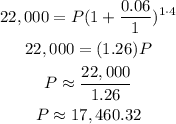
Hence, there must be deposited $17,460.32, approximately.

To find the annual payment, first, we find the total earnings through the 4 years.

`22,000-17,460.32=4,539.68`

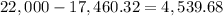
Then, we divide by 4

`(4,539.68)/(4)=1,134.92`

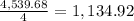
Hence, the annual payment is $1,134.92.