Question

A book is at rest, which statement is true?the options are below

Answer 1

The given problem can be exemplified in the following diagram:

Since the book is at rest we notice that the two forces acting are:

`\begin{gathered} N=\text{ normal force} \\ F_g=\text{ force of gravity} \end{gathered}`

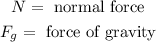
We can add the forces in the vertical direction and we get:

`\Sigma F_v=N-F_g`

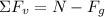
Since the book is at rest according to NEwton's second law the sum of forces must be equal to the product of the mass by the acceleration but the acceleration is zero, therefore:

`N-F_g=0`

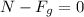
Adding the force of gravity to both sides:

`N=F_g`

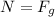
This means that the normal force balances the force of gravity.