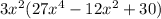Question

Factor out the GCF of the expression1.3x^3 + 9x2.81x^6 - 36x^4 + 90x^2

Answer 1

`1.\text{ }3x(x^2+3)`
`2.\text{ }3x^2(27x^4-12x^2+30)`

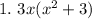
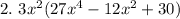
Step-by-step explanation

Given:

`\begin{gathered} Part\text{ 1. }3x^3+9x \\ Part\text{ 2. }81x^6-36x^4+90x^2 \end{gathered}`

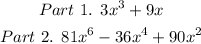
Determine the GCF of all the expression's terms

3: 1, 3

9: 1, 3, 9

36: 1, 2, 3, 4, 6, 9, 12, 18, 36

81: 1, 3, 9, 27, 81

90: 1, 3, 9, 10

Part 1:

The GCF = 3x

Then, to the left of a set of parenthesis, write the GCF: 3x( )

After that, divide each term in the original equation by the GCF (3x) and put it in parenthesis.

That is:

`\begin{gathered} (3x^3)/(3x)=x^2 \\ \frac{9x}{3x\text{ }}=3 \end{gathered}`

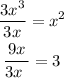
So you have:

`3x(x^2+3)`

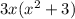
Part 2:

The GCF = 3x^2

`\begin{gathered} (81x^6)/(3x^2)=27x^4 \\ (36x^4)/(3x^2)=12x^2 \\ (90x^2)/(3x^2)=30 \end{gathered}`

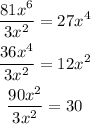
Hence, you have:

`3x^2(27x^4-12x^2+30)`