Question

Find the equation of the line that is parallel to the line x + 5y = 10 and passes through the point (1, 3). A) y 1 16 5 5 5 B) y = -5x - 16 C) y = 5x + 10 D) y=x-2

Answer 1

First, we need to take the equation x + 5y = 10 and solve for y as:

`\begin{gathered} x+5y=10 \\ 5y=10-x \\ y=(10-x)/(5) \\ y=2-(1)/(5)x \end{gathered}`

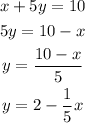
Since the coefficient of x is -1/5, the slope of this function is -1/5 and the slope of a parallel line is also -1/5.

Then, with the slope m and a point (x1, y1), we can find the equation of a line as:

`y-y_1=m(x-x_1)`

So, replacing m by -1/5 and (x1, y1) by (1, 3), we get:

`\begin{gathered} y-3=(-1)/(5)(x-1) \\ y-3=(-1)/(5)x-(1)/(5)\cdot(-1) \\ y-3=(-1)/(5)x+(1)/(5) \\ y=(-1)/(5)x+(1)/(5)+3 \\ y=(-1)/(5)x+(16)/(5) \end{gathered}`

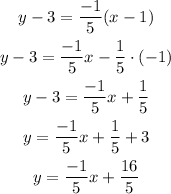
Answer: y = -(1/5)x + (16/5)