We need to first identify the center of the circle.
We see that the coordinate point of the center of the circle is (-1, -2).
The equation of a circle is given with the equation

where h is x, k is y, and r is the radius of the circle.
Therefore, we can plug in the coordinates first to find the h and k of the equation.
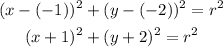
Then, we need to determine r.
The circle intersects points (-6, -2) and (4, -2). We can simply subtract the x-coordinates from each other to find the diameter of the circle.
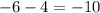
Finally, we know the radius is half of the diameter:
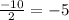
We can plug in the radius into the equation.

Therefore, our final equation is Choice D:
