Question

the cost of a ticket to the circus is 21.00 for children and 36.00 for adults on a certain day attendance at the circus was 19,000 and the total gate revenue was 56,400 how many children and how many adults bought tickets?the number of children was______The number of adults was____

Answer 1

We know that

• The ticket for children costs $21.

,

• The ticket for adults costs $36.

,

• There were 19 people.

,

• The total gate revenue is $56,400.

To solve this we have to form a system of linear equations. The first equation would be

`x+y=1,900`

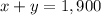
Where x is children and y is adults, there were 19 in total.

The second equation would be

`21x+36y=56,400`

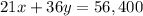
This equation represents the total earnings.

Let's isolate y in the first equation.

`y=1,900-x`

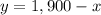
Now, we replace this expression in the second equation.

`\begin{gathered} 21x+36(1,900-x)=56,400 \\ 21x+68,400-36x=56,400 \\ -15x=56,400-68,400 \\ -15x=-12,000 \\ x=(-12,000)/(-15) \\ x=800 \end{gathered}`

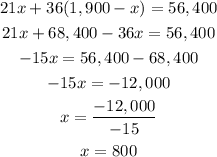
There were 800 children.

Then, we use this value to find y.

`\begin{gathered} y=1,900-x \\ y=1,900-800 \\ y=1,100 \end{gathered}`

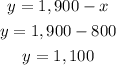
There were 1,100 adults.

Therefore, the number of children was 800, and the number of adults was 1,100.