To graph the solution set of the system, first, we have to graph each inequality.
First, express each inequality as an equation.
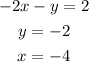
Then, graph each equation, they represent lines. The second and third equations are horizontal and vertical lines, respectively. While the first equation has an inclination, to graph the first one, we have to find the zeros of the equation.
Y - INTERCEPT (x = 0).

The y-intercept is (0,-2).
X - INTERCEPT (y = 0).
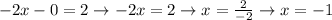
The x-intercept is (-1,0).
Using the intercept points, we can draw the line. Also, let's draw the other two.
Once we have all the lines, evaluate the inequalities to see which area is the solution.
y ≥-2 indicates that all the real numbers above or equal to -2 must be the solution.
x ≥-4 indicates that all the real numbers on the right of the line must be the solution.
Now, evaluate the first inequality with a test point (0,0).
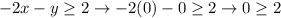
But, we know that zero is not greater than 2, which means the solutions must be below the red line because it can't include the point (0,0).
Unite all three areas to get the final solution set.
Therefore, the purple triangle represents the solution set.