The scenario would be represented by a given right angle triangle as shown below
Looking at the triangle,
BC = x represents the height of the tree
AC = x + 4 represents the length of the wire
AB = x - 28 represents the distance from the base of the tree to the wire.
We would solve for x by applying pythagorean theorem which states that
Hypotenuse^2 = shorter leg^2 + longer leg^2
hypotenuse = x + 4
shorterleg = x - 28
Longer leg = x
Thus, we have
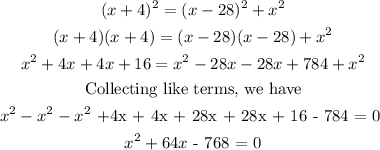
We would solve the quadratic equation by applying the general formula for solving quadratic equations which is expressed as
![\begin{gathered} x\text{ = }\frac{-\text{ b}\pm\sqrt[]{b^2-4ac}}{2a} \\ \text{From the equation, } \\ a\text{ = 1, b = 64, c = - 768} \\ x\text{ = }\frac{-\text{ 64 }\pm\sqrt[]{64^2-4(1*-768)}}{2*1} \\ x\text{ = }\frac{-64\pm\sqrt[]{4096\text{ + 3072}}}{2} \\ x\text{ = }\frac{-\text{ 64 }\pm84.66}{2} \\ x\text{ = }(20.66)/(2)\text{ or x = }\frac{-\text{ 148.66}}{2} \\ x\text{ = 10.3 or x = } \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/high-school/sccqbnyxojtbrwvupwrvsy1709b8gc3lrr.png)