Question

Here are the equations of five straight lines. Find the slope of each line.Line A y = 2x – 3 m=Line B 2y = x + 3 m =Line C 4y = 3x – 2 m = Line D 2y = 4x – 1 m = Line E 3y = 2x – 2 m =

Answer 1

Given,

The equation of lines are,

Line A y = 2x – 3

Line B 2y = x + 3

Line C 4y = 3x – 2

Line D 2y = 4x – 1

Line E 3y = 2x – 2

The standard equation of line is,

`y\text{ = mx+c}`

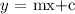
Here, m is the slope of the line and c is y - intercept.

Taking the line A as,

`y=2x-3`

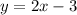
On comparing the line A with standard equation of line then the slope of the line is obtained m = 2.

Taking the line B as,

`\begin{gathered} 2y=x+3 \\ y=(x)/(2)+(3)/(2) \end{gathered}`

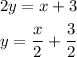
On comparing the line B with standard equation of line then the slope of the line is obtained m = 1/2.

Taking the line C as,

`\begin{gathered} 4y=3x-2 \\ y=(3x)/(4)-(2)/(4) \end{gathered}`

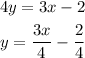
On comparing the line C with standard equation of line then the slope of the line is obtained m = 3/4.

Taking the line D as,

`\begin{gathered} 4y=3x-2 \\ y=(3x)/(4)-(2)/(4) \end{gathered}`

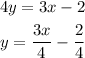
On comparing the line D with standard equation of line then the slope of the line is obtained m = 2.