To find a unit vector in the direction of a vector given we just need to divide it by its magnitude, that is:
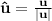
The magnitude of a vector is given by:
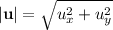
In this case we have:
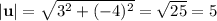
Hence the magnitude of the vector given is 5. Now that we know the magnitude of the vector we need to divide it by this. Therefore, to find a unit vector we multiply u by 1/5