We want to calculate the following division
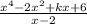
To efetuate this divison, we start by dividing the leading term of the dividend by the leading term of the divisor:
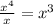
Then, we multiply this result by the divisor:
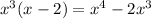
Then, subtract the dividend from the obtained result:
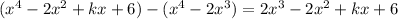
Then, we can rewrite our division as:
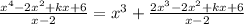
The remainder of this first division still have a polynomial on the dividend, therefore, we can iterate the previous process until we find the final result of this division.
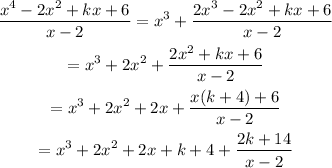
And this is the final result of the division.
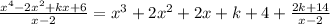
We want to find the value of k that will make the remainder equal to
The remainder of this division is
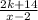
Then, we just need to solve for k the following equation
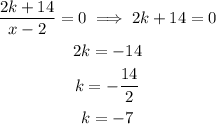
The value of k must be - 7.
.