Question

I'm not sure how to solve this question, I know how to find instantaneous rate of change but in this case I'm confused, I don't understand B.) as well

Answer 1

EXPLANATION :

a. The instantaneous rate of change is the same as the slope of the curve at a given point.

The slope function of f(x) is the first derivative of that function, f'(x)

From the problem, we have :

`g(x)=x^4-2x^3+1`

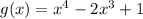
Calculate the first derivative :

`\begin{gathered} g(x)=x^4-2x^3+1 \\ g^(\prime)(x)=4(x^(4-1))-3(2x^(3-1))+0 \\ g^(\prime)(x)=4x^3-6x^2 \end{gathered}`

To find the solve at x = 1, evaluate g'(x) at x = 1

`\begin{gathered} g^(\prime)(1)=4(1)^3-6(1)^2 \\ g^(\prime)(1)=-2 \end{gathered}`

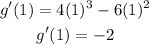
The instantaneous rate of change is -2

b. The instantaneous rate of change is constant at any x-value if the function is linear.

Since the given function is NOT a linear, then the instantaneous rate of change is NOT the same.