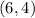First, find the equation of each line. Next, solve the system of equations to find the point at which those lines intersect.
The general equation of a line in slope-intercept form, is:

Where m is the slope of the line and b is the y-intercept.
On the other hand, given the coordinates of two points:

The slope of a line through those two points is given by:
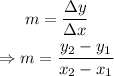
Find the equation of the first line in slope-intercept form. Using the coordinates (1,-1) and (5,3), calculate the slope:
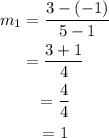
Substitute m=1 into the equation of a line in slope-intercept form:

Substitute the coordinates of a point into the equation to find the value of b. Use the point (1,-1), so that x=1 and y=-1:
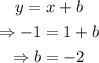
Therefore, the equation of the first line, is:
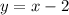
Using a similar method, we can find that the slope of the second line is:
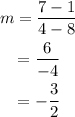
And the y-intercept will be given by:
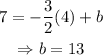
Therefore, the equation of the second line, is:
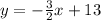
Substitute y=x-2 from the first equation into y in the second equation and solve for x to find the x-coordinate of the point at which these lines intersect.
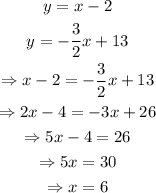
Substitute x=6 into y=x-2 to find the y-coordinate of the point at which these lines intersect:
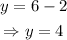
Since x=6 and y=4, therefore, the point at which these lines intersect, is: