To answer this question we will assume the following:
• The amount of gas is constant, that is, the moles do not change.
,
• The pressure remains constant.
,
• The gas behaves like an ideal gas.
With these assumptions, we can apply Charles's law which tells us:
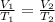
Where,
V1 is the initial volume of the gas in liters, 120mL=0.120L
T1 is the initial temperature in Kelvin, 27°C+273.15K=300.15K
V2 is the final volume of the gas in liters, 80.0mL=0.080L
T2 is the final temperature in Kelvin, unknown.
We clear T2 and replace the known data:

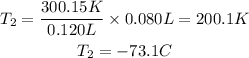
Answer: The gas would have a volume of 80.0mL at -73.1°C