Question

Use technology to find points and then graph the line y=\frac{5}{2}x+5,y= 25x+5, following the instructions below.IT CAN NOT BE GREATER than 10 AND IT CAN NOT BE FOR EXAMPLE 4.25 JUST A NUMBER

Answer 1

The given equation is

`y=(5)/(2)x+5`

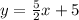
We will find 2 points on the line and use them to draw it

Let x = 0 and find the corresponding value of y

`\begin{gathered} y=(5)/(2)(0)+5 \\ y=0+5 \\ y=5 \end{gathered}`

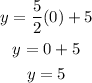
The first point is (0, 5)

Let y = 0 and find the corresponding value of x

`0=(5)/(2)x+5`

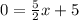
Subtract 5 from both sides

`\begin{gathered} 0-5=(5)/(2)x+5-5 \\ -5=(5)/(2)x \end{gathered}`

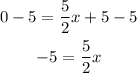
Multiply each side by 2

`\begin{gathered} -5(2)=(5)/(2)(2)x \\ -10=5x \end{gathered}`

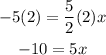
Divide both sides by 5

`\begin{gathered} (-10)/(5)=(5x)/(5) \\ -2=x \end{gathered}`

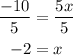
The second point is (-2, 0)

Let us draw the graph

The red line represents the given equation