Question

Which recursive sequence would produce the sequence 2,3, 7, ...?

Answer 1

`\begin{gathered} a_1=2\text{ and } \\ a_n=4a_(n-1)-5 \end{gathered}`

Step-by-step explanation:

Let's use the recursive sequence in each answer option and compare if the terms are 2, 3, 7,...

So, for option a, we get:

`\begin{gathered} a_1=2 \\ a_n=4a_(n-1)-5 \end{gathered}`

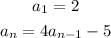
So, we can find a₂ and a₃ as follows:

a₂ = 4a₁ - 5

a₂ = 4(2) - 5

a₂ = 8 - 5

a₂ = 3

a₃ = 4a₂ - 5

a₃ = 4(3) - 5

a₃ = 12 - 5

a₃ = 7

Since this option satisfy the sequence a1 = 2, a2 = 3 and a3 = 7, we get that this is the correct answer.

So, the answer is the first option.