Question

Determine which of the given points lies on both of the lines in the system of equations by substituting each point into both equations.x - y = 53- 3x + y = -1

Answer 1

The system of linear equations is,

`\begin{gathered} x-y=5\ldots\ldots(1) \\ -3x+y=-1\ldots\ldots(2) \end{gathered}`

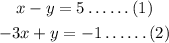
Consider the point (0,-1).

Check the first equation,

`LHS=0-(-1)=0+1=1\\e RHS`

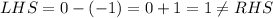
Since the point does not satisfy the equation (1), there is no need to check the other equation and it can be concluded that this point (0,-1) is not the point lying on both the lines.

Consider the point (3,8).

Check the first equation,

`LHS=3-(8)=3-8=-5\\e RHS`

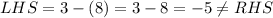
Since the point does not satisfy the equation (1), there is no need to check the other equation and it can be concluded that this point (0,-1) is not the point lying on both the lines.

Consider the point (-2,-7).

Check the first equation,

`LHS=-2-(-7)=-2+7=5=RHS`

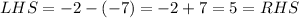
Check the second equation,

`LHS=-3(-2)+(-7)=6-7=-1=RHS`

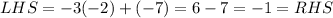
Here the point (-2,-7) satisfies both the equations. SO it can be concluded that the point is a common solution of the system of linear equations. Therefore, the point (-2,-7) will lie on both lines.

Consider the point (2,-3).

Check the first equation,

`LHS=2-(-3)=2+3=5=RHS`

Check the second equation,

`LHS=-3(2)+(-3)=-6-3=-9\\e RHS`

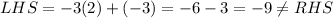
Since the point does not satisfy the equation (2), it can be concluded that this point (0,-1) is not the point lying on both the lines.