Question

Find the slope of each line and then determine if the lines are parallel, perpendicular or neither. If a value is not an integer type it as a decimal rounded to the nearest hundredth.Line 1: passes through (1,7) and (5,5) the slope of this line is Answer.Line 2: passes through (-1,-3) and (1,1) the slope of this line is Answer.The lines are Answer

Answer 1

As given by the question

There are given that the point of two-line

`\begin{gathered} (1,\text{ 7) and (5, 5)} \\ (-1,\text{ -3) and (1, 1)} \end{gathered}`

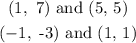
Now,

From the condition of a parallel and perpendicular line

If the slopes are equal then the lines are parallel

If the slopes are negative reciprocal then the lines are perpendicular

If the slopes are neither of the above are true then lines are neither

Then,

First, find the slope of both of line

So,

For first-line, from the formula of slope

`\begin{gathered} m_1=(y_2-y_1)/(x_2-x_1) \\ m_1=\frac{5_{}-7_{}}{5_{}-1_{}} \\ m_1=-(2)/(4) \\ m_1=-(1)/(2) \end{gathered}`

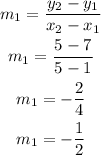
Now,

For second-line,

`\begin{gathered} m_1=(y_2-y_1)/(x_2-x_1) \\ m_1=\frac{1_{}-(-3)_{}}{1-(-1)_{}} \\ m_1=(4)/(2) \\ m_1=2 \end{gathered}`

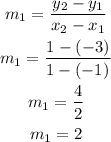
The given result of the slope is negative reciprocal because

`\begin{gathered} -(1)/(2)=-(-(2)/(1)) \\ -(1)/(2)=2 \end{gathered}`

Hence, the slope of line1 is -1/2, and slope of line2 is 2 and the lines are perpendicular.