We can model the radius function, R(t), with respect to time.
The initial radiusis 5 cm and it increases 7 cm /second, so we can write:
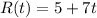
• At ,t = 4 ,second, the radius is:
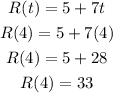
We can find the area of the spotlight by substituting r = 33 into the circle area formula. This is shown below:
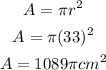
• At ,t = 7 ,second, the radius is:
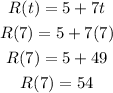
We can find the area of the spotlight by substituting r = 54 into the circle area formula. This is shown below:
