Question

Please help. I really need it.Tickets for all of the described charity raffle games cost $2. James wants to choose three raffles that will give him the best chance of winning. Identify the games that James should play and the games he shouldn't play.

Answer 1

Step-by-step explanation

From the statement, we know that we have different tickets for different games. We must select the three tickets with the best winning chances.

To select each ticket, we must consider two things:

0. its winning probability p,

,

1. its reward R.

We will compute the expected reward E of each ticket:

`E_i=R_i\cdot p_i,`

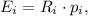
and select the three tickets with the highest rewards.

We label each ticket with a number:

In each game, we must pick three digits from 0 to 9 one after the other with replacement.

The total number of ways of selecting three numbers is n(total) = 1000.

We denote the winning events as W.

1) Ticket #1

The winning reward for this ticket is R₁ = $504.

In this case, there are only two ways of winning, so n(W) = 2.

The probability of winning with this ticket is given by:

`P_1=(n(W_i))/(n(total))=(2)/(1000).`

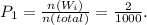
The expected reward for this case is:

`E_1=R_1\cdot p_1=\text{ \$504}\cdot(2)/(1000)=\text{ \$}1.008`

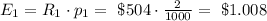
2) Ticket #2

The winning reward for this ticket is R₂ = $1152.

In this case, there is only one way of winning, so n(W) = 1.

The probability of winning with this ticket is given by:

`p_2=(1)/(1000).`

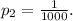
The expected reward for this case is:

`E_2=R_2\cdot p_2=\text{\$1152}\cdot(1)/(1000)=\text{ \$1.152.}`

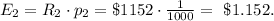
3) Ticket #3

The winning reward for this ticket is R₃ = $204.

In this case, the number of winning cases is given by the permutation with replacement of r = 3 digits from n = 10 digits:

`n(W)=P(n+k-1,n-1)=((n+r-1)!)/((n-1)!r!)=((10+3-1)!)/((10-1)!3!)=(12!)/(9!3!)=220.`

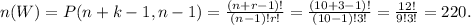
The probability of winning with this ticket is given by:

`p_3=(n(W))/(n(total))=(220)/(1000).`

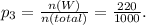
The expected reward for this case is:

`E_4=R_4\cdot p_4=\text{\$204}\cdot(220)/(1000)=\text{\$44.}`

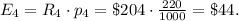
4) Ticket #4

The winning reward for this ticket is R₄ = $120.

In this case, there are 100 ways of winning, so n(W) = 100.

The probability of winning with this ticket is given by:

`p_4=(100)/(1000)=(1)/(10).`

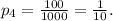
The expected reward for this case is:

`E_4=R_4\cdot p_4=\text{\$120}\cdot(1)/(10)=\text{ \$12.}`

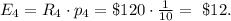
5) Ticket #5

The winning reward for this ticket is R₅ = $1500.

In this case, there is only one way of winning, so n(W) = 1.

The probability of winning with this ticket is given by:

`p_5=(1)/(1000).`

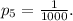
The expected reward for this case is:

`E_5=R_5\cdot p_5=\text{\$1500}\cdot(1)/(1000)=\text{ \$1.5.}`

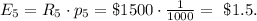
6) Ticket #6

The winning reward for this ticket is R₆ = $8.

In this case, there are 100 ways of winning, so n(W) = 100.

The probability of winning with this ticket is given by:

`p_6=(100)/(1000)=0.1.`

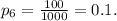
The expected reward for this case is:

`E_6=R_6\cdot p_6=\text{ \$8}\cdot0.1=\text{ \$0.8.}`

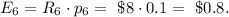
Comparing the results from about, and looking for the greatest expected earnings, we see that:

• the best games are: #3, #4 and #5,

,

• the worst games are: #1, #2 and #6.

Answer

Raffles that James should play are #3, #4 and $5.

Raffles that James shouldn't play are #1, #2 and #6.