Question

Q1: Henry used square papers, each measuring 1 square unit, to tile a rectangle with no gaps or overlaps. He sketched his work as shown. Use the image to fill in the missing information. 3 units 2 늘 Henry's rectangle: units long units wide Area = square units

Answer 1

Note that the side of each square is unity.

Along the horizontal, it has 3 complete squares, so the length of Henry's rectangle is 3 units,

`\begin{gathered} L=1+1+1 \\ L=3 \end{gathered}`

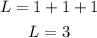
Along the vertical, it has 2 complete squares while 1 half heighted rectangle, so the width of Henry's rectangle is,

`\begin{gathered} W=1+1+(1)/(2) \\ W=1+1+0.5 \\ W=2.5 \end{gathered}`

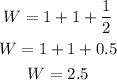
Solve for the area of the rectangle as,

`\begin{gathered} \text{Area}=\text{Length}*\text{ Width} \\ \text{Area}=3*2.5 \\ \text{Area}=7.5 \end{gathered}`

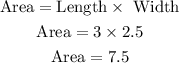
Thus, the Henry's rectangle is 3 units long, 2.5 units wide, and the area of the rectangle is 7.5 square units.