Question

When priced at $30, a toy has monthly sale of 4000 units. For each $1 increase in price, sells will decrease by 100 units. Find the maximimum total revenue possiblelevenue = Periso Gescentity [hinti price = (30 + 1x) and quanlity = (400-10Gx)

Answer 1

$122,500

1) Since the revenue is given by this product: price x quantity, we can write it out and plug into that the given data:

`\begin{gathered} R=P\cdot Q \\ R=(30+x)(4000-100x) \end{gathered}`

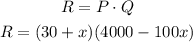
2) Now, let's expand those factors:

`\begin{gathered} R=(30+x)(4000-100x) \\ R=120,000-3000x+4000x-100x^2 \\ R=-100x^2+1000x+120,000 \end{gathered}`

The maximum total revenue is given by the y-coordinate on the Vertex of that parabola. Let's use another formula for that:

`Y_V=-(\Delta)/(4a)=(-(1000^2-4(-100)(120000)))/(4(-100))=122500`

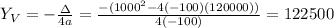
3) Hence, the maximum revenue would be $122,500