Question

A point is turning along the circular path with R = 30 cm at constant angular accelerationε. Find the tangential and total accelerations of the point if it made 3 revolutions for 4 s and its normal acceleration was 2.7 m/s2at this instant. Find the linear and angular velocities at this instant.

Answer 1

Givens.

• R = 30 cm.

,

• t = 4 seconds.

,

• a_n = 2.7 m/s^2.

,

• n = 3 revolutions.

First, we need to find the angular acceleration.

`\theta=\omega_ot+(1)/(2)\varepsilon t^2`

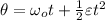
But, we need to find the angular displacement and the angular speed.

`\begin{gathered} \theta=3rev\cdot(2\pi)/(1rev)\cdot=6\pi \\ a_n=(v^2)/(R)\to v^2=a_n\cdot R=v=\sqrt[]{2.7\cdot(m)/(s^2)\cdot0.30m} \\ v=0.9\cdot(m)/(s) \end{gathered}`

The displacement of 3 revolutions is 6pi radians and the tangential (linear) speed of 0.9 m/s. Use the radius to find the angular speed.

`\begin{gathered} \omega=(v)/(R)=(0.9\cdot(m)/(s))/(0.30m) \\ \omega=3\cdot\frac{\text{rad}}{\sec } \end{gathered}`

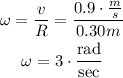
Once we have the angular speed and the angular displacement, we are able to find the angular acceleration.

`\begin{gathered} \theta=\omega_ot+(1)/(2)\varepsilon t^2 \\ 6\pi=3\cdot4+(1)/(2)\cdot\varepsilon(4)^2 \\ 6\pi=12+6\varepsilon \\ \varepsilon=(6\pi-12)/(6) \\ \varepsilon\approx1.14\cdot(rad)/(\sec ^2) \end{gathered}`

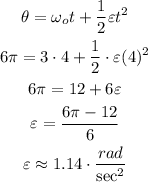
Once we have the angular acceleration, we can find the tangential acceleration.

`a_t=\varepsilon R=1.14\cdot0.30\approx0.34\cdot(m)/(s^2)`

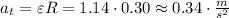
The tangential acceleration is 0.34 m/s^2.

The total acceleration would be

`\begin{gathered} a_{\text{total}}=\sqrt[]{a^2_t+a^2_n}=\sqrt[]{(0.34)^2+(2.7)^2} \\ a_{\text{total}}=\sqrt[]{0.1156+7.29}\approx2.72\cdot(m)/(s^2) \end{gathered}`

The total acceleration is 2.72 m/s^2.

The linear velocity is 0.9 m/s.

The angular velocity is 3 rad/sec.