Question

can you help me to do this oneBambook recorded the sale of their books from last quarter and found outthat 45 percent of all published books were fiction. If you pick seven books at random from a book store. what's the probability that either none or one of them is non-fiction?i need 4 digit decimals answer.

Answer 1

Since we only have two possible outcomes here: either fiction or non-fiction books, we are dealing with binomial probability. The formula for this is:

`_nC_x* p^x*(1-p)^(n-x)`

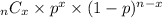
where n = the number of trials, x = number of successes, p = probability of a success on an individual trial.

Now, based on the question, here are the information:

the number of trials (n) = 7 random books

probability of getting a fiction book on an individual trial = 45%

probability of getting a non-fiction book on an individual trial (p) = 55%

There are two written successes in the question:

a. 0 non fiction book (x)

b. 1 non fiction book (x)

Let's solve first the probability of getting zero non-fiction books. Let's plug in the given data to the formula above.

`\begin{gathered} _nC_x* p^x*(1-p)^(n-x) \\ _7C_0*0.55^0*0.45^(7-0) \\ 1*1*0.00373669 \\ =0.00373669 \end{gathered}`

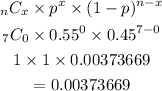
The probability of getting zero non-fiction book is 0.00373669.

Let's now solve the probability of getting 1 non-fiction book. x = 1.

`\begin{gathered} _nC_x* p^x*(1-p)^(n-x) \\ _7C_1*0.55^1*0.45^6 \\ 7*0.55*0.008303765 \\ =0.031969 \end{gathered}`

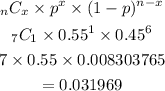
The probability of getting 1 non-fiction book is 0.031969.

So, the probability of getting 0 OR 1 non-fiction book is:

`0.00373669+0.031969=0.0357`

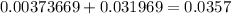
The probability of getting 0 OR 1 non-fiction book is 0.0357.