The given function is,
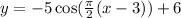
The graph can be drawn as,
The period will be distance between two consequetive maximas,
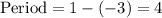
Thus, period is correct.
The amplitude can be determined as,
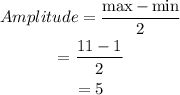
Thus, amplitue is incorrect.
The range is,
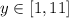
Thus, the range is correct.
The midline is,
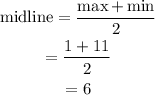
Thus, the midline is correct.
Thus, option (b) is the solution.