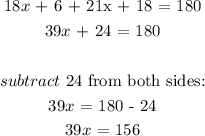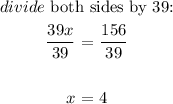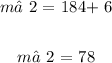Answer:
m∠2 = 78°
Step-by-step explanation:
Given:
m∠2 = (18x + 6)°
m∠3 = (21x + 18)°
To find:
m∠2
From the diagram, m∠2 and m∠3 are the same side interior angles. Same-side interior angles sum up to 180 degrees as they are supplementary angles. As a result,
m∠2 + m∠3 = 180°
(18x + 6)° + (21x + 18)° = 180°