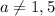We have the following rational expression:
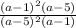
And we have to reduce the expression to the lowest terms.
1. To achieve that, we can see that:
• There are two common factors:
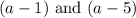
2. Now, we know that:

3. And we can apply the same rule for the given case as follows:
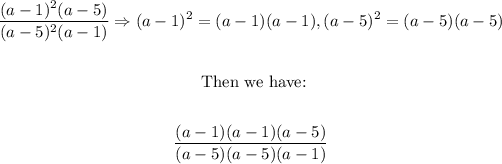
4. And we can rewrite the expression as follows:
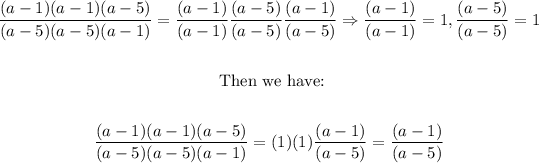
Therefore, the rational expression of the lowest terms is:
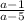
5. We can determine that the variable restrictions for the original expression can be found as follows:
![\begin{gathered} ((a-1)^(2)(a-5))/((a-5)^(2)(a-1)) \\ \\ \text{ If a = 5, then we would have:} \\ \\ ((a-1)^2(5-5))/((5-5)^2(a-1))=(0)/(0)\rightarrow\text{ This is NOT defined. Then a}\\e5 \end{gathered}]()
![\begin{gathered} ((a-1)^(2)(a-5))/((a-5)^(2)(a-1)) \\ \\ \text{ If a = 1, then we have:} \\ \\ ((1-1)^2(a-5))/((a-5)^2(1-1))=(0)/(0)\rightarrow\text{ This is NOT defined. Then a}\\e1 \end{gathered}]()
Therefore, in summary, we have that:
• The rational expression in the lowest terms is:
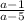
• The variable restrictions for the original expression: