I need help with A and B please and thank you.

Question

asked Oct 28, 2023 205k views

1 Answer

Abdul Wahab · Answer 1 · 2023-11-02T03:33:29+0000

Given:

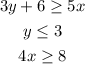
$\begin{gathered} 3y+6\ge5x \\ y\leq3 \\ 4x\ge8 \end{gathered}$

And we have that:

$\begin{gathered} 4x\ge8 \\ (4x)/(4)\ge(8)/(2) \\ x\ge4 \end{gathered}$

Therefore, both together imply that:

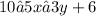
So we get that:

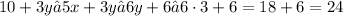
$10+3y≤5x+3y≤6y+6≤6\cdot3+6=18+6=24$

since we are given that y ≤ 3, so we also get:

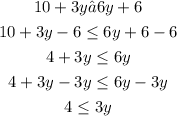
$\begin{gathered} 10+3y≤6y+6 \\ 10+3y-6\leq6y+6-6 \\ 4+3y\leq6y \\ 4+3y-3y\leq6y-3y \\ 4\leq3y \end{gathered}$

Now we have:

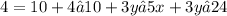
and then also the following:

a) The maximum of Q = 5x + 3y is 24, and the minimum of Q is 14.

Answer:

Maximum = 24

Minimum = 14

b) The new maximum would be the negative of the original minimum, and the new minimum would be the negative of the original maximum, therefore:

This is:

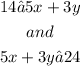
$\begin{gathered} 14≤5x+3y \\ and \\ 5x+3y≤24 \end{gathered}$

Then we can multiply both sides of both inequalities by -1, but we have to switch the direction of these inequalities:

$\begin{gathered} 14(-1)\leq5x(-1)+3y(-1) \\ -14\leq-5x-3y \end{gathered}$

And

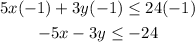
$\begin{gathered} 5x(-1)+3y(-1)\leq24(-1) \\ -5x-3y\leq-24 \end{gathered}$

0r put in the correct order, from smallest to largest, we get:

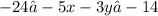
Answer:

Maximum = -14

Minimum = -24