Given the equation:
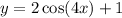
Let's graph the equation.
Apply the form:
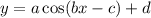
Where:
a = 2
b = 4
c = 0
d = 1
Let's determine the amplitude, period, phase shift and vertical shif.
Amplitutde = a = 2
To find the period, we have:
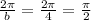
Phase shift:
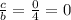
Vertical shift, d = 1
Find few points of the equation on a graph.
We have:
When x = 0
y = 2 cos (4(0))+1
y = 2 cos (0)+1
y = 2 (1) + 1
y = 2 + 1
y = 3
When x = π/8
y = 2 cos (4(π/8)) + 1
y = 2 cos(π/2) + 1
y = 2 (0) + 1
y = 0 + 1
y = 1
When x = π/4
y = 2 cos(4(π/4))+1
y = 2 cos(π) + 1
y = 2 (-cos(0)) + 1
y = 2(-1) + 1
y = -2 + 1
y = -1
WHen x = π/2
y = 2 cos(4(π/2)) + 1
y = 2 cos(2π) + 1
y = 2 cos(0) + 1
y = 2(1) + 1
y = 2 + 1
y = 3 =
Thus, we have the points:
(0, 3), (π/8, 1), (π/4, -1), (π/2, 3)
The graph of the equation is attached below: