Solve the equations (the answer might be no solution or all real numbers)4(A + 4) - 9(A - 4)= 3711=7 - (1- y)3+7(p - 10)= - 38 -(5 -3p)20 + 5(3-5A)= -5(A-6)+5

Question

asked Aug 7, 2023 99.0k views

1 Answer

Harjatin · Answer 1 · 2023-08-12T16:43:17+0000

Solution:

Consider the following equations:

Equation 1:

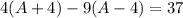
$4\mleft(A+4\mright)-9\mleft(A-4\mright)=37$

Equation 2:

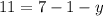
Equation 3:

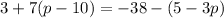
$3+7\mleft(p-10\mright)=-38-\mleft(5-3p\mright)$

Equation 4:

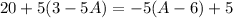
$20+5\mleft(3-5A\mright)=-5\mleft(A-6\mright)+5$

From equation 1, we get:

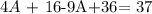
$4A\text{ + 16-9A+36= 37}$

this is equivalent to:

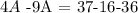
$4A\text{ -9A = 37-16-36}$

this is equivalent to:

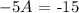
$-5A\text{ = -15}$

solving for A, we get:

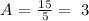
$A\text{ = }(15)/(5)=\text{ 3}$

then A = 3.

From equation 4, we get:

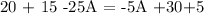
$20\text{ + 15 -25A = -5A +30+5}$

this is equivalent to:

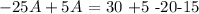
$-25A+5A\text{ = 30 +5 -20-15}$

this is equivalent to:

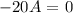
$-20A\text{ = }0$

Thus A = 0.

But this is a contradiction since we had found that A =3. Then, the linear system has no solution (is incongruent).