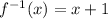Question

Find the inverse of the function. Graph the function and its inverse.f(x) = x - 2/2

Answer 1

We need to find the inverse of the funcion:

`f\mleft(x\mright)=x-2/2`

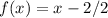
Notice that:

`(2)/(2)=1`

Thus, we have:

`f(x)=x-1`

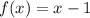
Now, to find its inverse, we can follow the steps below:

• replace x with y;

,

• replace f(x) with x;

,

• isolate y on the left side;

,

• replace y with f⁻¹(x).

We obtain:

`\begin{gathered} x=y-1 \\ \\ y-1=x \\ \\ y-1+1=x+1 \\ \\ y=x+1 \\ \\ f^(-1)(x)=x+1 \end{gathered}`

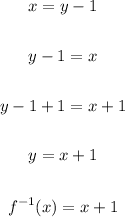
Now, we need to graph both f(x) and f⁻¹(x).

In order to graph f(x), since it is a line, we can plot two points of the form (x, f(x)) and then join those points to form the line:

`\begin{gathered} f(0)=0-1=-1\text{ point }(0,-1) \\ \\ f(1)=1-1=0\text{ point }(1,0) \end{gathered}`

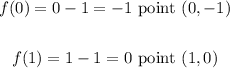
Similarly, to graph f⁻¹(x), we can do as follows:

`\begin{gathered} f⁻¹\left(0\right)=0+1=1\text{ point }(0,1) \\ \\ f⁻¹\left(1\right)=1+1=2\text{ point }(1,2) \end{gathered}`

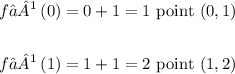
Answer:

`f^(-1)(x)=x+1`