A line can be written with the equation:

Where m is the slope and b is the y-intercept.
Lines that are paralle have the same slope, m, and different values for b.
So, if we get the graph for one line, we can:
- find the slope of the original line
- the slope of the paralle line is the same, so we also found it already.
- choose a point of b that gives a line different from the one before.
Let (x₁, y₁) and (x₂, y₂) be points on the original line. Thus, the slope m will be:

From the graph of the original line, we can choose these 2 points. Let's choose these:
Which are (0, -5) and (-3, 1). Using them into the formula, we have:
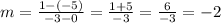
So, the slope of the original line is -2 and (0, -5) is the y-intercept, so b = -5 and the equation of the line is:
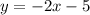
Now, the slope of the parallel line is the same, so the slope of the parallel line is -2.
Since we can choose any parallel line to draw (different from the given one), we can choose the simplest one, which will have b = 0 and equation:
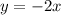
So, we can get two points in it:
x = 0:
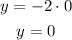
And x = -3:
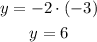
So, the graph will be: