Question

The perimeter of a rectangular garden is 316 feet. If the length of the garden is 97 feet, what is its width?

Answer 1

To answer this question we will set and solve an equation.

Recall that the perimeter of a rectangle is given by the following formula:

`Perimeter=2length+2width.`

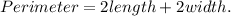
Substituting Perimeter=316feet and length=97feet we get:

`316ft=2*97ft+2width.`

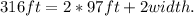
Simplifying the above result we get:

`316ft=194ft+2width.`

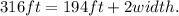
Subtracting 194ft from the above equation we get:

`\begin{gathered} 316ft-194ft=194ft+2width-194ft, \\ 122ft=2width. \end{gathered}`

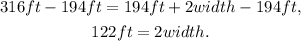
Dividing the above equation by 2 we get:

`\begin{gathered} (122ft)/(2)=(2width)/(2), \\ 61ft=width. \end{gathered}`

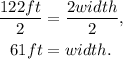
Answer: 61 feet.