This corresponds to a sinusoidal graph, we have:
Radius= 20 feet, that corresponds to the amplitud (A)
One revolution takes 24 seconds, that corresponds to the period
Min= 3 feet
k=360/24=15
D= bottom distance+ amplitud=3+20=23 feet
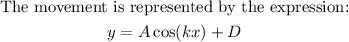
Then, let x be the time, in seconds:
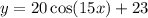
a) To determine Reid's height after 1 minute= 60 seconds, substitute x=60
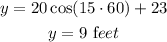
b) To determine when Reid's height will first reach 18 feet, we have to substitute y=18 feet, and isolate x:
