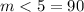Could someone please help me solve this question? Thanks! (Click image to see question)

Question

asked Dec 6, 2023 39.2k views

1 Answer

Natt · Answer 1 · 2023-12-13T02:55:26+0000

We will have the following:

*First: From properties of the rhombus the following is true:

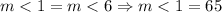
$m<1=m<6\Rightarrow m<1=65$
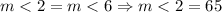
$m<2=m<6\Rightarrow m<2=65$

*Second: We know that the sum of all internal angles of a quadrilateral add 360°, so the following is true:

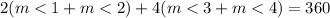
So:

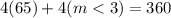
This, since from properties of the rhombus m<3 = m<4, now we wil have:

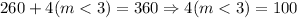
$260+4(m<3)=360\Rightarrow4(m<3)=100$
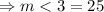
$\Rightarrow m<3=25$

Now, we will have the following:

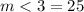
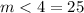
And finally, we can see that the measurement of angle 5 is: