Question

Find the slope of the line containing the points (4,8) and (4,6) then find the slope of a line parallel to this line and the slope of the line perpendicular to this line.

Answer 1

1. not defined
2. not defined
3. zero

Explanation:

The question is asking us to find the slope.

First, we will find the slope of the line that passes through (4,8) and (4,6).

We'll use the slope formula:

`\bf{m=(y_2-y_1)/(x_2-x_1)}`

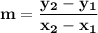
Plug in the data :

`\bf{m=(6-8)/(4-4)}`

`\bf{m=(-2)/(0)}`

`\bf{m=not\:de fined}`

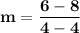
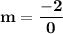
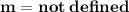
If a line's slope is not defined, then it's a vertical line:

`\rule{1}{350}`

------

Now, what is the slope of a line that's parallel to the one above? Well, since parallel lines have equal slopes, that one will have an undefined slope too.

As for perpendicular lines, they have slopes that are negative reciprocals of each other. We got that the slope is -2/0. The negative reciprocal of that is 0/2, which simplifies to 0.

Alternatively, you could look at it this way: a horizontal line (a line with zero slope) is perpendicular to a vertical line. So the slope of that line is m = 0.

`\rule{350}{1}`

Answer 2

To calculate the slope between 2 points we use the following equation:

`m=(y_2-y_1)/(x_2-x_1)`

Replacing the points:

`\begin{gathered} m=(8-6)/(4-4) \\ m=(2)/(0) \\ m\to\infty \end{gathered}`

In this case, when we find an infinite slope, it means that it is a line parallel to the Y axis. All parallel lines have the same slope.

For the perpendicular case, the slope is equal to:

`\begin{gathered} m_(\perp)=(1)/(m) \\ m_(\perp)=(1)/((2)/(0)) \\ m_(\perp)=(0)/(2) \\ m_(\perp)=0 \end{gathered}`

For the perpendicular case, the slope is zero and would equal one parallel to the X axis.