Question

How many moles of CH3CH2Cl are contained in 250 mL of 0.0666 M CH3CH2Cl solution?

Answer 1

We can find the number of moles using the molarity formula:

`\text{Molarity}=\frac{moles}{volume\text{ (liters)}}.`

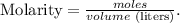
We have to convert 250 mL to L. Remember that 1 liter equals 1000 mL:

`250\text{ mL}\cdot\frac{1\text{ L}}{1000\text{ mL}}=0.25\text{ L.}`

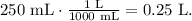
Now, that we have the value of volume in liters (0.25 L) and the molarity (0.0666 M (mol/L) ), we can clear in the formula for moles and replace the given values:

`\begin{gathered} \text{moles}=\text{Molarity}\cdot\text{volume,} \\ \text{moles}=0.0666(mol)/(L)\cdot0.25L, \\ \text{moles}=0.0166\text{ moles=1.66}\cdot10^(-2)moles. \end{gathered}`

The answer is that we have 1.66 x 10^(-2) moles in 0.25 L of 0.0666 M of CH3CH2Cl.