Question

Angle A is complementary to Angle B, Angle B is supplementary to Angle C, and the ratio of Angle A to Angle C is 11:26. Find the measurements of Angle B.

Answer 1

Since the complementary angles have a sum of 90 degrees

Since

`A+B=90^(\circ)\rightarrow(1)`

Since the supplementary angles have a sum of 180 degrees

Since

`B+C=180^(\circ)\rightarrow(2)`

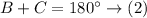
Subtract (1) from (2) to eliminate B

`\begin{gathered} (B-B)+(C-A)=(180-90) \\ C-A=90\rightarrow(3) \end{gathered}`

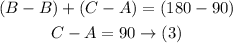
Since the ratio between A and C is 11: 26

Then the difference in ratio between C and A is

`\begin{gathered} C-A=26x-11x \\ C-A=15x\rightarrow(4) \end{gathered}`

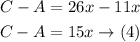
Equate (3) and (4) to find x

`15x=90`

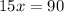
Divide both sides by 15

`\begin{gathered} (15x)/(15)=(90)/(15) \\ x=6 \end{gathered}`

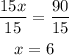
Substitute x in the ratio of A and C to find them

`\begin{gathered} A=11x \\ A=11*6 \\ A=66^(\circ) \end{gathered}`

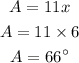
Substitute it in equation (1) to find B

`66+B=90`

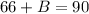
Subtract 66 from both sides

`\begin{gathered} 66-66+B=90-66 \\ B=24^(\circ) \end{gathered}`

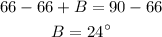
Angle B is 24 degrees