SOLUTION
Let us make a graph for the table. For this graph, we will take the first year (1990) as 0 and each subsequent year by adding 2 to the previous ones
The graph is shown below.
We can see that it is a line graph that slopes downwards.
Hence, the graph is linear.
The model for the graph is given as
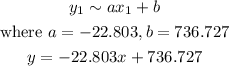
Hence, the graph model is
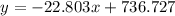
What year will number of unemployed reach 5?
We will use the graph model to determine this.
This becomes

Now, since we took 1990 as 0, the year when the number of unemployed will be 5 becomes

Hence, the answer is year 2022