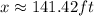A Right triangle is a triangle that has an angle whose measure is 90 degrees.
A 45°-45°-90°-degree triangle is a Right triangle that has two angles that measure 45 degrees. This triangle has two sides of equal length.
You can identify that the triangle given in the exercise is a 45°-45°-90°-degree triangle.
According to the 45°-45°-90° Triangle theorem:
![hypotenuse=\sqrt[]{2}\cdot leg](https://img.qammunity.org/2023/formulas/mathematics/high-school/3caz0m81gtfb57wk5cytw2bycljd1z3k7q.png)
In this case:
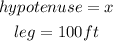
Substituting values into the equation and evaluating, you get that length of the path will be the following:
![\begin{gathered} x=(\sqrt[]{2})(100ft) \\ x=100\sqrt[]{2}ft \\ x\approx141.42ft \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/high-school/tnipgfnqovjvmlzz2fggtdc6mevf136s4l.png)
The answer is: