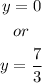We need to find the solution to the equation
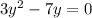
Step 1
Rewrite the expression on the left side, grouping the common factor, as follows:
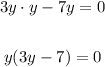
Step 2
Notice that the above equation holds when one of the factors is zero:

Answer
Since both 0 and 7/3 are already reduced to the lowest terms, the answer is