This problem has a composit function:
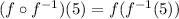
This means that we have to find the value of the function "f" when the input is "f^-1(5)". In this case the input function is the inverse. Inverses are functions that invert the domain and range of the original function. This means that if we we calculate "f^-1(5)" we will find which value on the range of the inverse that is related to 5 on the domain, but on the original function the domain and range are inverted, so we will obtain the following result:
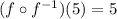
The value is 5.