Question

A 6.25-gram bullet travels at 365 m/s. It hits and enters a 4.50-kg crate. The crates slide 0.15 m along a floor until it comes to rest.a. What is the speed of the crate/bullet system immediately after the collision?b. What is the change in kinetic energy of the system after the collision?c. Find the friction force between the crate and the floor.

Answer 1

a.

The momentum is defined as:

`p=mv`

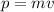
We know that, in a collision, the momentum of the system is conserved; this means that:

`p_i=p_f`

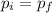
In this case we have that:

`m_bv_b+m_cv_c=(m_b+m_c)v`

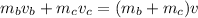
Plugging the values given we have that:

`\begin{gathered} (0.00625)(365)+(4.5)(0)=(0.00625+4.5)v \\ v=((0.00625)(365))/((0.00625+4.5)) \\ v=0.506 \end{gathered}`

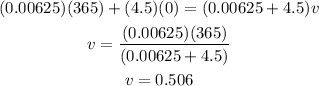
Therefore, the velocity of the system after the collision is 0.506 m/s.

b.

The kinetic energy is given by:

`K=(1)/(2)mv^2`

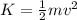
The total initial kinetic energy is:

`\begin{gathered} K_i=(1)/(2)m_bv^2_b+(1)/(2)m_cv^2_c \\ K_i=(1)/(2)(0.00625)(365)^2+(1)/(2)(4.5)(0)^2 \\ K_i=416.33 \end{gathered}`

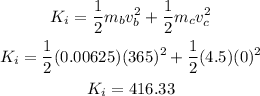
The total final kinetic energy is:

`\begin{gathered} K_f=(1)/(2)(m_b+m_c)v^2 \\ K_f=(1)/(2)(0.00625+4.5)(0.506)^2 \\ K_f=0.577 \end{gathered}`

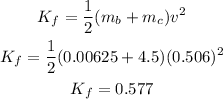
The change in kinetic energy is given by:

`\Delta K=K_f-K_0`

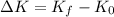
Then in this case we have:

`\begin{gathered} \Delta K=0.577-416.33 \\ \Delta K=-415.753 \end{gathered}`

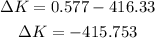
Therefore the change in kinetic energy is -415.753 J

c.

From Newton's second law we know that the resultant force is related to the mass and the acceleration as:

`\vec{F}=m\vec{a}`

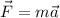
For this situation, in the x-direction, the only force exerted on the crate/bullet system is the force of friction, then we have:

`-f=ma`

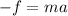
then, to determine the force of friction we need the acceleration.

To determine the acceleration we can assume that from the moment the system slide to where it stops the motion is an uniform accelerated motion, then we can use:

`v^2_f-v^2_0=2ad`

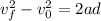
plugging the values and solving for the acceleration we have:

`\begin{gathered} 0^2-0.506^2=2a(0.15) \\ a=-(0.506^2)/(2(0.15)) \\ a=-0.853 \end{gathered}`

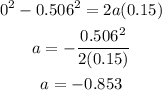
Now that we have the acceleration we have that:

`\begin{gathered} -f=(0.00625+4.5)(-0.853) \\ f=3.84 \end{gathered}`

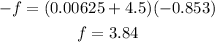
Therefore the force of friction is 3.84 N (Remember that it points to the left, this is express in the equation of motion)