The initial population is P(0) = 600.
The carrying capacity for the pond is K=1500.
The rate of growth is r=1.4 (or 140%).
As this model is described by the logistic equation, we can write:
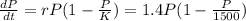
We can solve this differential equation as:

We can substitute the variables as:
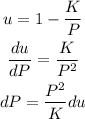
Replacing in the integral:
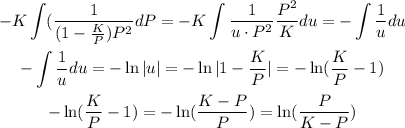
The other integral is solved as:
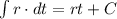
Then, we can write:
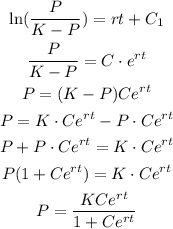
We can find the value of the constant C using the information of the initial condition:
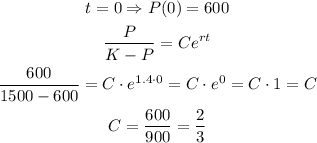
Then, the model becomes:
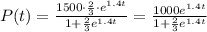
For the first season (t=1), the population will be:
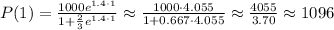
After the second season (t=2), the population will be:
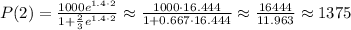
Answer:
Population after the first season P(1) = 1096 fish.
Population after the second season P(1) = 1375 fish.