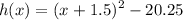The function is given as
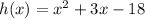
Step 1: Divide the coefficient of x by 2 and square it then add to 3x and then subtract from -18
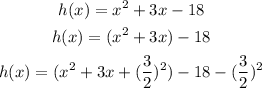
Step 2: Combine the squares and then simplify the fractions to decimal

Hence,
The final answer is
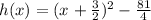
In decimal, it can be written as