Question

Hank has some 60% maple syrup and some 80% maple syrup in his restaurant. How manyounces of each should he use to make 100 ounces of 75% maple syrup?

Answer 1

Let x be the amount of used ounces of the 60% maple syrup and y the amount of used ounces of the 80% maple syrup.

We will mix this two quantities so we get 100 ounces. That is, we add both quantities to get 100 ounces, so we have the equation

`x+y=100`

Now, we want to find the second equation to find x and y. To do so, we will calculate the amount of maple we have.

In x ounces of the mixture, we would have

`0.6\cdot x`

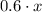
of maple syrup.

For the other mixture, we would have

`0.8\cdot y`

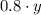
The sum should be equal to the total amount of maple we have in the new mixture. Since we have a total of 100 ounces and a concentration of 75% we would have

`100\cdot0.75`

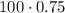
So, by adding the previous results and making it equal to this last amount, we get

`0.6\cdot x+0.8\cdot y=100\cdot0.75=75`

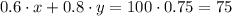
To avoid decimals, we can multiply this equation by 10, so we have

`6x+8y=750`

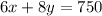
Using the first equation we can find that

`x=100\text{ -y}`

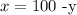
If we replace this value in the second equation, we get

`6\cdot(100\text{ -y)+8y=750}`

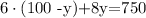
Distributing on the left side, we get

`600\text{ - 6y+8y=750}`

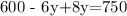
Operating on the left side, we get

`600+2y=750`

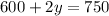
By subtracting 600 on both sides ,we get

`2y=750\text{ -600=150}`

By dividing both sides by 2 we get

`y=(150)/(2)=75`

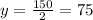
If we replace this value in the equation we found for x, we get

`x=100\text{ -75 = 25}`

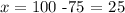
So, we need to mix 25 ounces of the first maple syrup and 75 ounces of the second one to get the desired mixture.