We have an exponential decay model expressed as:
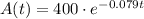
We can express the the decay as the variation between consecutive terms, like A(t+1) and A(t), relative to a A(t).
We can express this as:
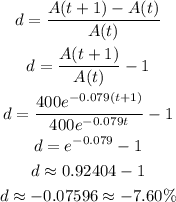
We then can conclude that the decay for this model is 7.60%.
NOTE: the decay d is negative as A decreases with the increase in t.
Answer: the decay percentage is 7.60%.